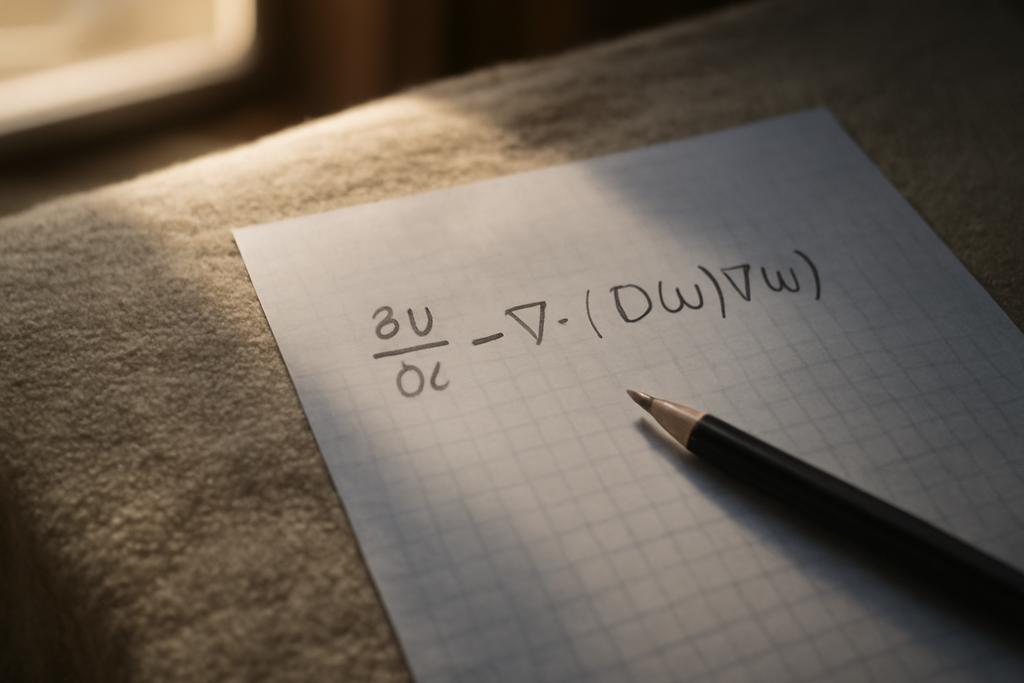In the real world, materials and environments aren’t the same from one corner to the next. Diffusion—whether it’s heat moving through a composite, chemicals seeping through soil, or even how a population spreads—depends on the local properties of the medium. If you change the texture of the fabric, you change how fast heat travels. If you gradient the density of a habitat, you change how a population swells or settles. The math that underpins these realities is stubbornly nonlinear and surprisingly delicate when the rules shift across space.
A recent piece of mathematical science leans into that mess with clarity and ambition. University of Craiova mathematician Maxim Bogdan and his collaborators study a class of problems that couple two kinds of nonlinear behavior: a diffusion mechanism whose strength can change from place to place (a so‑called variable exponent) and a growth term—the logistic source—that can also warp in nonstandard ways. The resulting equation is what researchers call a doubly nonlinear elliptic problem with variable exponents and homogeneous Neumann boundary conditions. The study asks a foundational question: under very weak assumptions, can we guarantee a well-behaved steady state, and can we know it’s unique? The answers are surprisingly robust, and the method used to get them—discretizing time and solving a cascade of elliptic problems—offers a blueprint for how to tame the unruly math of spatially variable media.
What follows is a guided tour of the paper’s core idea, why it matters, and what’s new and potentially transformative about it. The work is rooted in rigorous functional analysis, but its implications ripple through physics, biology, materials science, and even image processing—where the same math that describes a steady population density can also model how an image evolves under diffusion with spatially varying sharpness. The authors are explicit about one thing: this is not an off‑the‑shelf recipe for every problem, but a carefully constructed framework that works under broad, realistic conditions. And it’s anchored in a real institution—Maxim Bogdan’s team at the University of Craiova in Romania—so the ideas have a stable home as they’re tested and extended.
A New Equation for Changing Realities
The heart of the work is an abstract, yet richly interpretable, parabolic problem: a time‑dependent, or evolutionary, equation in which the rate at which something diffuses can itself depend on the gradient of the unknown, and that dependence can vary from point to point in space. Concretely, the model features a nonlinear diffusion term a(x, ∇u) and a nonlinear reaction or source term f(x, u). The diffusion is built from a function Ψ(x, |∇u|) that assigns a diffusion strength that can change with location and with how steeply u climbs in space. When you sit down and “freeze” time, you get a related elliptic problem: the steady states solve −div a(x, ∇V) + λ b(x, V) = g(x) with the boundary condition a(x, ∇V) · ν = 0 on the boundary, and where λ is a positive parameter that scales the nonlinear reaction term b(x, V). This particular shape is what mathematicians call a doubly nonlinear elliptic problem, because the two nonlinear pieces—the diffusion and the reaction—are simultaneously in play and both depend on the unknown function in nontrivial ways.
Space isn’t uniform here. The p(x) framework lets the model’s diffusion “p‑growth” exponent vary with location. In a simple p‑Laplacian, diffusion strength scales like |∇u|p−1; here that exponent is p(x), a function of position. That’s not just technical flourish: physically, it captures media where the mechanism that relays, say, heat or a chemical signal, changes with the tissue type, soil texture, or material microstructure. The mathematics has to cope with this extra layer of complexity, ensuring the theory still behaves when the exponents creep up and down across the domain.
To wrestle with the problem, Bogdan and coauthors lean on Rothe’s method, a time‑discretization strategy that solves a sequence of elliptic problems step by step to approximate the full parabolic problem. Think of walking through a time ladder: you fix a time increment, solve the steady snapshot at that moment, then move to the next, and so on. If each rung is well‑behaved and the ladder is built with care, you get a well‑posed, continuous evolution in time. In the paper, Rothe’s method isn’t just a trick; it’s a bridge that allows the authors transfer existence and uniqueness results from the elliptic (steady) world to the parabolic (time‑dependent) world under very mild hypotheses on the source term f and the logistic‑type nonlinearity b.
One of the striking moves in this work is to relax a staple assumption that often appears in nonlinear PDE literature: the source term f is locally Lipschitz. This is a strong, technical condition that can cut away many physically plausible models. Bogdan’s framework replaces it with a much weaker monotonicity assumption and a careful analysis of the Nemytskii operator—the rule that takes a function v(x) and returns f(x, v(x))—in spaces where the exponent p can vary with x. The upshot is a result that holds in a broad, realistic range of scenarios, including ones where the nonlinearity grows or recedes in a non‑Lipschitz fashion as u changes. In other words, the math no longer demands a strict smoothness that real‑world sources often lack.
Crucially, the core results aren’t merely existence statements. The paper also secures uniqueness of steady states under precise structural conditions, and it does so using energy functionals crafted from the problem’s nonlinear ingredients. The functional framework introduces auxiliary problems (for instance, a λ‑scaled elliptic problem) and uses a clever blend of monotonicity, convexity, and lower semicontinuity to pin down a unique minimizer. This is where the abstract math becomes a tool for predicting the behavior of complex systems: the steady states aren’t just some abstract solutions; they’re the energy‑minimizing configurations that systems naturally settle into under fixed environmental parameters.
From Theory to Steady States: Why It Matters
Why should a mathematician care about steady states, and why should scientists outside the math department care about the details of how they’re proved? Because steady states are the long‑term blueprint of dynamic processes. In biology, a population’s density in an environment with spatially varying resources may settle into a stable distribution. In materials science, a chemical or thermal field might reach a fixed profile given the material’s inhomogeneities. In image processing, diffusion models are used to smooth images while preserving edges, with spatially varying diffusion capturing the idea that some regions should blur more than others. The doubly nonlinear, variable‑exponent framework is a robust umbrella under which all these stories can be told with a single mathematical language.
The paper doesn’t just prove that a steady state exists; it also ensures that, within a broad class of constraints, there is a well‑ordered structure of steady states. There can be a minimal and a maximal steady state in a given interval [ε, δ], and every other steady state in that band sits between them. That ordering is not a cosmetic detail. It mirrors how natural systems often behave: densities or concentrations cannot wander arbitrarily; they’re squeezed between physical bounds (think nonnegativity of population, or an environmental carrying capacity). The mathematics formalizes this intuition and shows it holds even when the usual niceties (like Lipschitz continuity of the source) are absent.
Another pillar of the work is the handling of the boundary. The authors impose homogeneous Neumann boundary conditions, meaning there’s no net flux across the domain’s boundary. This is a natural choice for closed systems—no matter leaks in or out—like a habitat with perfectly reflective edges or a sealed material sample. Getting a robust theory under Neumann conditions is trickier than under Dirichlet (where the boundary values are fixed), because the total mass is not pinned down by the boundary. Bogdan’s results show that even in this less forgiving setting, you can still guarantee existence and uniqueness of steady states, as long as the nonlinearities obey the structural assumptions laid out in the paper.
The logistic flavor in the source term f and the accompanying b term—the oft‑cited “generalized logistic source”—are more than cosmetic choices. They encode a population‑like growth that slows as density increases, a kind of environmental resistance that’s ubiquitous in biology and ecology, as well as in certain chemical and physical processes. The generality here matters: the authors don’t require a single rigid growth law. They only require monotonicity and a controlled growth pattern, which makes the theory applicable to a wide array of real situations where the interaction between diffusion and growth isn’t neatly linear or Lipschitz‑controlled.
Why the Results Are Notably Surprising (and What They Hint At)
Two strands of novelty jump out. First, the relaxation of the Lipschitz condition on f is not a small technical adjustment; it’s a doorway to models that were previously hard to place on solid mathematical ground. Real systems don’t always play nice: sources can jump, saturate, or behave unpredictably near boundaries or in regions with extreme properties. The fact that the authors can still guarantee a unique steady state under such relaxed assumptions is a strong statement about the resilience of the mathematical framework in the face of messy reality. The key technical move is to rely on the continuity of the Nemytskii operator between Lebesgue spaces with variable exponents, a carefully tuned piece of functional analysis that respects spatial heterogeneity without requiring the kind of uniform smoothness that standard hypotheses demand.
Second, the ability to treat a generalized logistic source in this variable‑exponent setting is a real conceptual leap. The logistic principle—growth that levels off as density grows—feels intuitively universal, but marrying it to a diffusion law that itself morphs with location is nontrivial. The authors show that, even when f is nonLipschitz and the diffusion’s exponent p(x) varies, there remains a coherent structure: a well‑defined, unique steady state in the right interval. And in a broader perspective, the paper doesn’t stop at a single steady state. It also demonstrates a broader existence theory for subinterval problems (DE[ε, δ]) and shows how minimal and maximal steady states arise naturally, a feature that resonates with how ecosystems or materials might settle into a spectrum of stable configurations depending on the chosen bounds. The mathematical machinery—energy functionals, Γ‑convergence arguments, and carefully designed auxiliary problems—reads as a blueprint for similar nonlinear, nonuniform PDEs you might encounter in other fields.
The work also unfolds a practical extension: a multi‑phase version of the problem where diffusion is a blend of several p(x)‑Laplacian components, each weighted by a spatially varying coefficient. This “MP” model speaks directly to materials with several dominant diffusion mechanisms or to ecological settings where multiple processes compete. The analysis shows that as long as the exponents stay within broad, physically meaningful bounds, the same existence/uniqueness theory can be ported to this richer, more realistic setting. It’s a demonstration that the framework is not a one‑trick pony but a flexible scaffold for a family of complex diffusion‑growth systems.
All of this, of course, rests on precise mathematical foundations. The paper builds a careful hierarchy of functionals—A, B, F, C, and D variants—each encoding a piece of the energy or mass balance. It then shows how these functionals interact to produce a coherent, closed loop: a weak solution exists, is nonnegative and bounded, and, under suitable monotonicity and convexity conditions, is unique inside the chosen interval. The results come with a robust toolbox: monotonicity methods, convexity arguments, and the idea that the diffusion and reaction parts are not just compatible but mutually reinforcing in yielding a single, stable outcome. That blend—rigor plus relevance—helps translate a complicated PDE into a tool that scientists can lean on when building or analyzing complex, heterogeneous models.
Throughout, the paper keeps a human touch: it foregrounds the idea that PDEs with variable exponents are not esoteric curiosities but natural mirrors of real materials and ecosystems. The math isn’t just about proving theorems in isolation; it’s about ensuring that the models we rely on to describe how things spread, grow, and settle into a steady pattern behave in ways we can trust, even when the environment itself isn’t uniform. And behind it all stands a concrete institution and a concrete mind: Maxim Bogdan of the University of Craiova, whose work here sharpens how we think about diffusion and growth in a changing world.
Bottom line: this work provides a solid, broadly applicable foundation for studying steady states in highly nonlinear, spatially variable systems. It shows that even when the usual niceties fall away, the mathematics can still guarantee predictable, unique outcomes that match our intuition about bounded, stable configurations. That’s not just a win for theory; it’s a signal that the models we’ll rely on to understand, design, and control complex, heterogeneous systems have a trustworthy bedrock to stand on.
Looking ahead, the methods and results could influence how researchers approach problems as diverse as gradient materials in engineering, diffusion‑limited processes in biology and ecology, and image processing algorithms that need to adapt diffusion strength across an image. The paper’s framework—where diffusion strength can vary in space, where the source term can be nonLil Lipschitz but monotone, and where steady states sit neatly within a chosen interval—offers a versatile lens for turning messy real‑world phenomena into solid mathematical insight. And it does so without sacrificing the rigorous underpinnings that give engineers and scientists the confidence to rely on these models in practice.
In the end, Bogdan’s doubly nonlinear elliptic problem is less about a single equation and more about a community of problems that share a common DNA: nonlinearity, spatial variation, and the stubborn, beautiful question of what a system looks like when it settles after a long, dynamic dance. The University of Craiova’s team has given us a map for that landscape, one that should help future researchers chart even more of the terrain without getting lost in the weeds of every local irregularity.