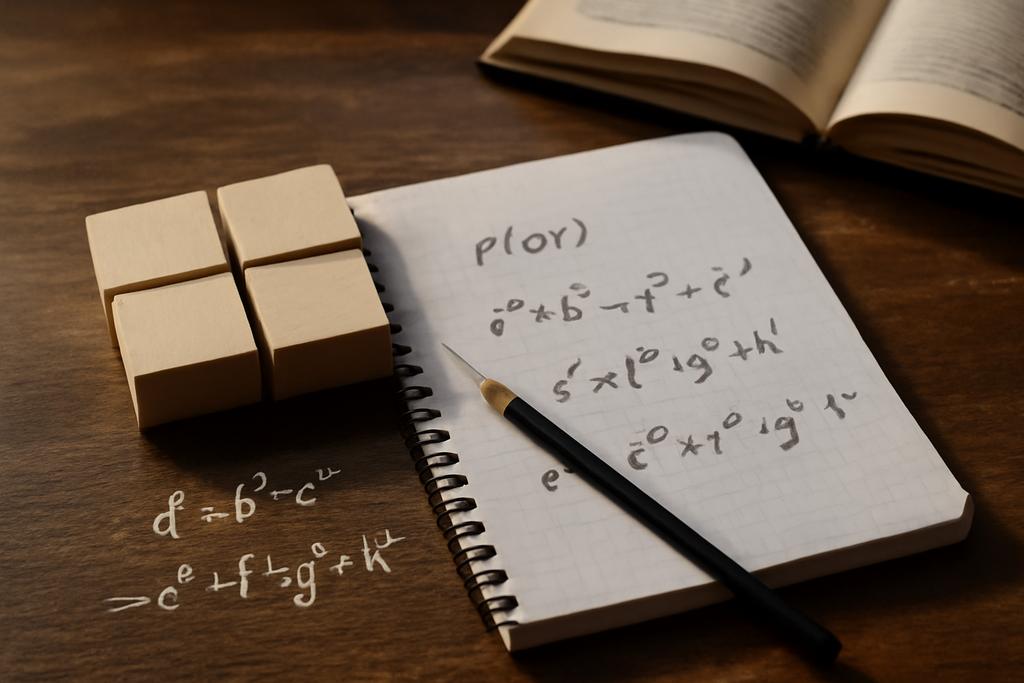The question of how many squares it takes to build every sum of squares is both ancient and modern in the same breath. In the familiar integers, a celebrated theorem—Lagrange’s four-square theorem—tells us any natural number is a sum of four squares. But step into the richer land of algebraic number fields, and the answer isn’t fixed. It depends on the field’s very structure. In particular, this paper dives into totally real biquadratic fields, rings of integers where the arithmetic can be as delicate as a piano of four strings, yet tuned by deeper number theoretic rules. The object of study is the Pythagoras number P(OK), the smallest n such that every sum of squares in the ring OK can be written as a sum of at most n squares. The question is not just a numeric curiosity; it’s a window into how additive building blocks behave when the universe itself is expanded from the rationals to a higher-dimensional setting.
The author, Daniel Dombek, writing from the Czech Technical University in Prague, Department of Applied Mathematics, tackles a long-standing conjecture pattern about biquadratic fields. The conjecture, built in part by Krasenský, Raška, and Sgallová, suggests a clean dividing line: P(OK) should be at least 6 for almost all totally real biquadratic fields that avoid certain small square roots, with only finitely many exceptions. The new work sharpens that line in two of the most stubborn corners of the map: fields that contain the square roots of 6 or 7, and, with substantial computational evidence, those containing the square root of 3. The upshot is a tighter, more explicit catalogue of which fields need six or more squares to express sums of squares, and which rare fields might slip below that threshold.
As a reader, you don’t need to be fluent in all the algebraic machinery to feel the punchline. It’s a story about how a simple arithmetic question—how many building blocks of squares do you need?—gets tangled when you move from ordinary numbers to the more exotic terrain of algebraic number theory. And it’s a story of how computation and theory come together to map a landscape that’s been outpacing intuition for decades. The Czech Technical University in Prague stands behind this line of inquiry, with Dombek guiding a careful mix of algebra, geometry of numbers, and computer-assisted search to peel back the layers of these biquadratic fields.
A map of sums of squares in biquadratic fields
To orient the reader, a biquadratic field K is built by adjoining to the rational numbers two square roots, say sqrt m and sqrt s, where m and s are square-free and greater than 1. There is a third square-free number t that completes the field in a symmetric way, but the essential geometry is that K sits inside a four-dimensional space over the rationals, with a natural basis that often looks like (1, sqrt m, sqrt s, sqrt t). The ring of integers OK is the arithmetic playground where questions about sums of squares come to life. The Pythagoras number P(OK) tells us how many squares we suddenly need to guarantee that any sum of squares in OK can be assembled from no more than that many pieces.
Over the last few years, a body of work has carved out the general shape of this landscape. We know that P(OK) never exceeds seven for biquadratic fields and that in many fields, you can push the lower bound up to six. The tricky border lands are those fields that happen to contain certain square roots, particularly sqrt 2, sqrt 3, sqrt 5, sqrt 6, and sqrt 7. These fields can behave quite differently from their siblings where those roots are absent. The latest results build on that map, identifying large swaths where P(OK) is forced to be at least six, while pinpointing precise families where the conjectured finite exceptions may live.
The paper marks a clear milestone: it fully solves two of the three remaining classes of biquadratic fields with respect to when P(OK) crosses the threshold of six. Specifically, for fields that contain sqrt 6 or sqrt 7, the author proves that, save for finitely many exceptions, P(OK) is at least six. The argument blends intricate Diophantine reasoning—where one writes an algebraic number as a sum of six squares and analyzes the resulting coefficient equations—with heavy computational work that checks many possible representations. The result is a robust push toward a clean dichotomy, matching the conjectured boundary and narrowing the still-open corners of the chart.
New thresholds and finite exceptions
The centerpiece theorems advance a crisp narrative about where exactly the six-square barrier holds. Theorem 2.1 says: if your biquadratic field does not contain sqrt 2, sqrt 3, or sqrt 5, then P(OK) is at least six, with a single explicit exception, namely K6,14. In other words, removing a handful of troublesome square roots from the field makes the six-block ceiling almost universal. The exceptional K6,14 stands out as a rare counterexample in an otherwise uniform landscape, and it becomes a focal point for future refinement of the conjecture.
Theorem 2.2 narrows the doorways for the stubborn sqrt 3 family. For fields K3,s with 17 ≤ s ≤ 511, the Pythagoras number jumps to at least six, with only eight potential outliers. Even more strikingly, when s is congruent to 1 modulo 4, the bound P(OK) ≥ 6 holds for huge swathes of s up to 15000 and across several large gaps. These computationally supported patterns reinforce the idea that the push from five to six is not a fluke but a delimited regime, with a tight, explicit list of exceptional cases that can be checked and, in principle, resolved.
Beyond theorems, the paper sketches a refined conjecture. Conjecture 2.3 posits a neat division: P(OK) ≤ 5 happens exactly when the field hosts sqrt 2 or sqrt 5, or when the field is among a short list of K3,s and K6,14 in which the six-square representation fails in a systematic way. If this holds, the boundary lines drawn by six vs five squares would correspond to concrete arithmetic fingerprints of the field, making the boundary between “easy” and “hard” sums of squares almost like a map legend that you can read directly from the field’s roots.
To accompany the theory, the author reports on the computational scaffolding that makes these arguments credible. A Python tool crafted by Raška and colleagues, along with Mathematica scripts and Magma checks, tests the possible six-square representations against the ring of integers in a wide range of fields. The message is not that the math is merely numerical; it’s that the structural reasoning—parity constraints, coefficient matching, and the geometry of the basis—must align with the computational search for the pattern to hold. The work is a clear example of how modern number theory often stands on a bridge between deep ideas and careful, large-scale computation.
How the proof dances with numbers
At the technical heart of the paper is a dance with what it means to express an algebraic number as a sum of squares. The author stages a six-square witness: pick an element that is a sum of six squares and analyze all possible ways to rewrite it as a sum of five or fewer squares. If one can show that no such rewriting exists, then that element certifies that P(OK) is at least six. The clever trick is to pick witnesses that force a web of Diophantine equations, built from the field’s integral basis, to collide in impossible ways unless at least six squares are needed.
The proof masterfully uses the integral bases of the different types of biquadratic fields, classified by congruences of m and s mod 4. Each type leads to a distinct system of equations when you equate traces and square coefficients. In practice, this means slogging through high-dimensional parity and divisibility considerations, then reducing the possibilities until only the six-square option survives. In several cases, one can push a direct, hand-checkable argument, but in the more intricate families, the author relies on computational verification to certify that certain length-6 representations are indeed minimal. The author notes explicitly what was computed, and what remains as a conjectural frontier for the case m = 3, where the story is subtler and more delicate to close.
The upshot is both a proof skeleton for large swaths of fields and a carefully documented cutting edge where calculations buttress theory. The work does not claim an ultimate classification of P(OK) for every biquadratic field, but it does move us closer to a satisfying dichotomy: most fields with sqrt 6 or sqrt 7, or with certain sqrt 3 configurations, require at least six squares, while a handful of exceptional fields likely land at five or below. The computational results supporting Conjecture 2.3 also map out concrete targets for future work—fields to test, witnesses to search for, and deeper structural explanations to uncover.
What this means for math, and why it matters
Why should curious readers care about Pythagoras numbers in such abstract settings? Because these questions are a window into how the additive and multiplicative fabrics of number fields mesh together. Sums of squares touch a constellation of ideas: representations of numbers, the geometry of numbers, and the way arithmetic behaves when you enlarge the field from Q to a richer arena. In practical terms, understanding P(OK) contributes to the broader project of understanding universal quadratic forms over rings of integers, which in turn links to questions about diophantine equations, cryptography, and the arithmetic of manifolds that underlie modern math.
Another layer of importance lies in the method. The field has progressed not just by proving theorems in isolation but by building robust computational ecosystems that test conjectures to exhaustion, then feeding that data back into theory. The collaboration between software like Magma and Raška’s Python tool and human insight is a microcosm of how contemporary mathematics operates today. The paper demonstrates that computer-aided exploration can illuminate which structural barriers are real and which might crumble under further cleverness or new ideas, a pattern that is increasingly common across pure math.
Finally, the work emphasizes a hopeful message for number theory: there is not merely a wilderness of unknowns but a lattice with recognizable, hopefully finite, fractures. The central conjecture hints that the boundary between five and six is not a philosophical mystery but a phenomenon governed by precisely which square roots live inside the field. If Conjecture 2.3 holds, then the landscape of biquadratic fields organizes itself around a small set of fingerprints. That would be a kind of arithmetic elegance: a complicated world that, at heart, respects a tidy boundary.
The study is a milestone in the long-running exploration of Pythagoras numbers in biquadratic fields, and it highlights two key themes for readers: first, that even tiny changes in the defining numbers of a field can ripple into big changes in arithmetic; and second, that modern number theory thrives on a dialogue between deep theory and computational verification. The Czech Technical University in Prague, through Dombek’s work, adds a precise, testable chapter to a story that’s been unfolding for decades: the story of how many squares we actually need to build the numbers that live in higher-dimensional arithmetic universes.
Lead institution and author: The research was conducted at the Czech Technical University in Prague, Department of Applied Mathematics, led by Daniel Dombek. This work builds on a tradition of exploring the additive structure of rings of integers in biquadratic fields, while pushing the frontiers with explicit computations and careful theoretical reasoning.