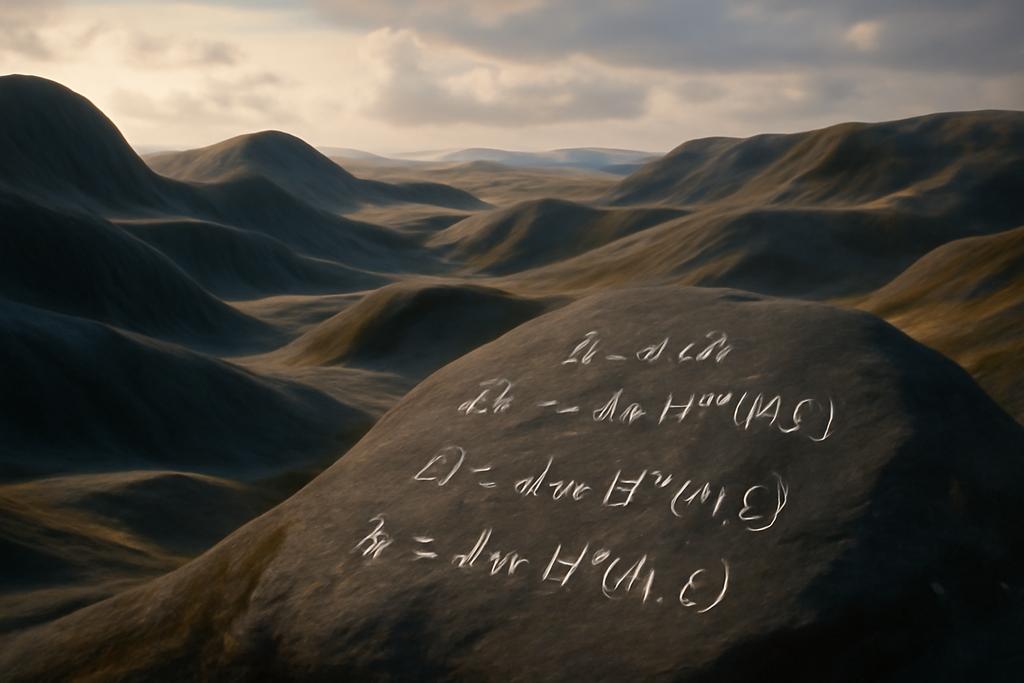Imagine a landscape sculpted not of earth and stone, but of intricate mathematical structures. This is the realm of complex manifolds, spaces that blend the familiar geometry of our world with the added twist of complex numbers. These spaces are crucial in understanding fundamental aspects of physics and topology, yet their hidden properties remain elusive. Recently, a breakthrough in mathematics sheds new light on these abstract realms, revealing a deeper connection between topology and complex geometry.
Unraveling the Fr”olicher Inequality
At the heart of this discovery lies the Fr”olicher inequality, a fundamental relationship between two key characteristics of a complex manifold. The first is the Betti number, which describes its topological connectivity – essentially, how many separate pieces it contains and how those pieces are linked together. It’s like a topological fingerprint of the space. The second is the Hodge number, a more refined measure that captures the complexity of the manifold from a complex geometric perspective. Imagine this as reflecting the manifold’s internal structure.
The Fr”olicher inequality states that the Betti numbers are always less than or equal to a specific combination of the Hodge numbers. For decades, the standard proof relied on a sophisticated mathematical tool called the Fr”olicher spectral sequence. This method, while powerful, can be technically challenging to grasp.
Francesco Bei and Riccardo Piovani, from Sapienza University of Rome, have now offered an alternative, more direct path to proving the Fr”olicher inequality. Their approach builds upon the concepts of harmonic forms, which essentially represent the ‘stable’ or ‘equilibrium’ states of a given space. It’s like finding the most naturally occurring patterns within the manifold’s structure. By cleverly manipulating these harmonic forms, they’ve created a new, spectral-sequence-free proof that is considerably simpler and more intuitive.
Beyond Compact Spaces: Exploring Infinite Coverings
The researchers didn’t stop at compact manifolds – spaces that are finite and well-behaved. Their work elegantly extends to the realm of infinite coverings, often visualized as endlessly repeating tilings of a compact space. These infinite spaces present unique mathematical challenges. For example, notions such as Betti and Hodge numbers – normally finite in compact spaces – need to be redefined for infinite ones using the concept of Von Neumann dimension.
This new approach uses what’s called the Von Neumann dimension, a tool that cleverly adapts standard ideas of dimension to fit the peculiar nature of these infinite spaces. By deftly incorporating this framework, Bei and Piovani show that their refined proof of the Fr”olicher inequality carries over elegantly to these intricate, infinitely extending spaces. They prove an analogous Fr”olicher inequality for these L2 Betti and Hodge numbers – a significant generalization of the original result.
The Power of Spectral Projectors and a Family of Operators
A critical element of Bei and Piovani’s approach involves a family of self-adjoint operators, which essentially transform forms on the manifold in a controlled and reversible manner. Think of them as a set of lenses, each providing a slightly different perspective on the same underlying space. The researchers build an injection – a one-to-one mapping – using so-called spectral projectors linked to these operators. These projectors skillfully isolate and highlight specific components of the manifold’s structure, revealing the deeper connections between Betti and Hodge numbers.
The proof’s ingenuity lies in proving the convergence of this family of operators. This convergence is established in the norm resolvent sense, a concept that assures the stable and consistent behavior of the operators as they transition from one perspective to another within the family. The convergence allows them to build the crucial injection between the relevant spaces, leading to the proof of the L2 Fr”olicher inequality.
Implications and Open Questions
This elegant new proof offers more than just mathematical sophistication. It opens avenues for further exploration of complex manifolds and related concepts, particularly in spaces that are not compact. The researchers themselves highlight several open questions, including a potential ‘L2-∂∂-Lemma’, analogous to a well-known result in compact manifolds. This Lemma would elegantly tie together different cohomology theories in the context of these infinite spaces.
The possibility of extending this work to study the behavior of these L2 invariants under deformations of the complex structure is particularly tantalizing. The upper semi-continuity of these invariants would provide crucial insights into the stability of the manifolds’ structures under small changes.
Bei and Piovani’s work demonstrates the ongoing push to understand the deeply intertwined nature of topology and complex geometry. Their new proof, elegant in its simplicity and far-reaching in its implications, represents a significant step forward in this journey of mathematical discovery.