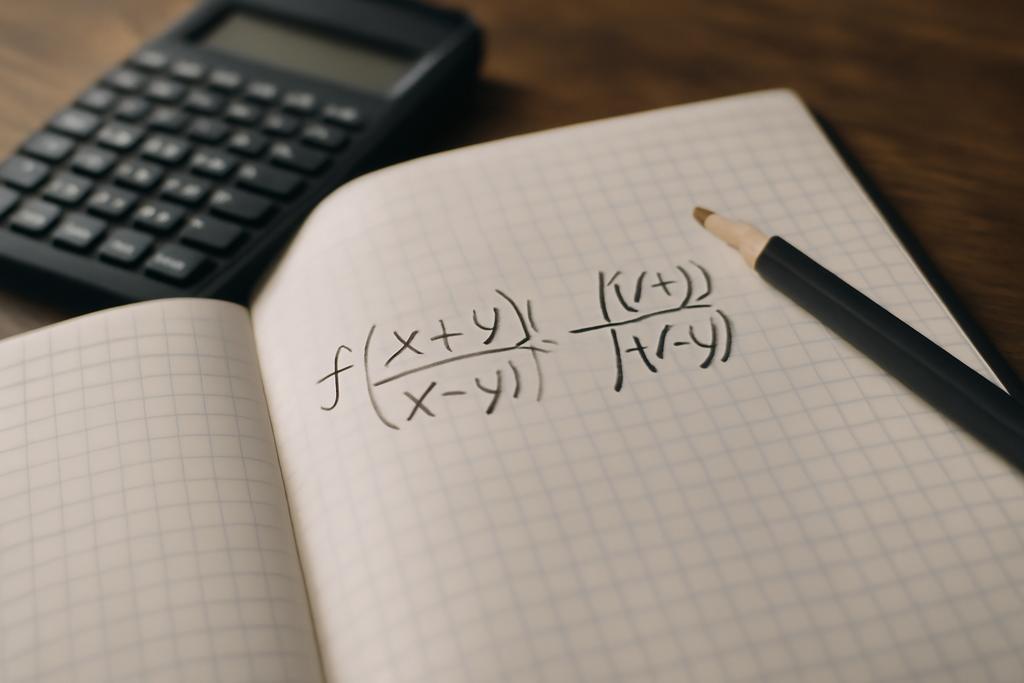Imagine a simple equation, so straightforward it could almost be an exercise for a freshman math major. Yet, it holds within it the potential to unlock deep secrets within different mathematical fields, from the realm of continuous functions to the intricate structures of algebraic number fields. This is the story of the Sum-Difference ratio preserving maps (SD maps) and the surprising discoveries made by Sunil Chebolu, Apoorva Khare, and Anindya Sen in their recent paper.
The Sum-Difference Equation
The heart of their work lies in a functional equation: f((x+y)/(x-y)) = (f(x)+f(y))/(f(x)-f(y)). This seemingly modest equation asks: what functions f, operating on a field (like the rational or real numbers), preserve this particular ratio of sums and differences? It’s a variation on the famous Cauchy functional equation, which has a simple solution if we assume the function is continuous, but whose discontinuous solutions are famously chaotic. In contrast, the researchers found something remarkably elegant and constrained in the case of SD maps. Their investigation is inspired by Cauchy’s functional equation; it explores how modifying the Cauchy equation gives rise to new types of functional equations with vastly different properties.
Unveiling Unexpected Order
The researchers’ findings are surprising. In the case of real numbers, the only solution—without making any assumptions about continuity—turns out to be the identity function: f(x) = x. Think about it: this seemingly arbitrary equation, imposing a condition on the ratio of sums and differences, essentially boils down to asserting that a function must be itself. It is as if the function is forced to behave in the simplest possible way, reflecting its intrinsic properties. This result holds for the rational numbers as well, and extends to a larger class of fields known as Euclidean subfields of the real numbers, which include constructible numbers (those built from 1 using a ruler and compass) and real algebraic numbers.
The researchers then explored the world of complex numbers. Here, they found two solutions: the identity function and the conjugate function (which switches the sign of the imaginary part of a complex number). The stunning part? These are the same solutions that appear when considering the field automorphisms of the complex numbers, which are far more complicated to define and analyze. This unexpected relationship indicates a potentially deep connection between the SD maps and field automorphisms.
A Mathematical Detective Story
The elegance of the results is matched by the researchers’ clever approach. They start by showing that any SD map must have several properties, such as injectivity (different inputs have different outputs), mapping 0 to 0, being an odd function (f(-x) = -f(x)), and being multiplicative (f(xy) = f(x)f(y)). These properties are derived through a series of insightful algebraic manipulations of the functional equation itself, like a mathematical detective carefully piecing together clues.
Building upon these properties, they then turn to more sophisticated mathematical tools to further investigate the case of real and complex numbers. For real numbers, they show that the SD maps are strictly increasing functions, and this, combined with the fact that they fix all rational numbers (another insightful observation), leads directly to the conclusion that the only solution is the identity function.
Their work on complex numbers is equally impressive, drawing on both algebraic and topological techniques. The approach is divided into two main parts: first they consider cases where the SD map preserves the real numbers, followed by cases where continuity is assumed. In the end, they show that the identity function and the complex conjugate function are the only possible solutions.
Beyond the Expected
However, the story doesn’t end with the beautiful results for real and complex numbers. The authors challenge the expectation that SD maps might coincide with field automorphisms by constructing counter-examples: specific SD maps that are not field automorphisms. These counter-examples show that the SD map equation defines a distinct class of functions. This emphasizes the power of their findings: the SD equation isn’t simply a rephrasing of a previously understood concept, but rather a gateway to a whole new area of mathematical investigation.
This exploration leads to exciting open questions. The researchers leave the reader with several intriguing challenges, such as investigating SD maps over finite fields and exploring the deeper connections between the SD equation and various branches of mathematics. Their work highlights that even simple-looking equations can harbor profound mathematical depth, and that the journey of discovery can often lead to unexpected and beautiful results. The paper, authored by Sunil Chebolu of Illinois State University, Apoorva Khare of the Indian Institute of Science, and Anindya Sen of the University of Otago, serves as a testament to the power of combining different mathematical techniques and approaching problems with fresh insight.