In the quiet corners of mathematics where shapes grow teeth and personality, convex lattice polytopes are not just pretty pictures. They are shapes built from the integer grid, with vertices sitting neatly on lattice points. Think of them as geometric fossils shaped by the arithmetic of Z4 or Z3 and so on, where every corner lies on an integer coordinate and every face curves into the lattice world. The study of when two such polytopes are actually the same shape in disguise is a question that blends geometry, algebra, and a dash of detective work.
Now imagine a transformation that moves every lattice point to another lattice point, without tearing the grid apart. A unimodular affine transformation does exactly that: it maps the integer lattice onto itself while reshuffling the polytope in space. The unimodular isomorphism problem UIP asks a deceptively simple question with deep consequences: given two convex lattice polytopes P and P prime, can we find such a unimodular map that carries P onto P prime? The beauty and the trap lie in the answer. If two polytopes are related by this grid-friendly reshaping, they share volume and lattice point structure; if not, they inhabit different unimodular worlds.
Backing this exploration is a team from the Center for Applied Mathematics at Tianjin University, led by Qiuyue Liu and Zhanyuan Cai. Their work elevates a classical question about when geometric shapes are the same under grid-preserving transformations and threads it through the loom of graph theory, cryptography, and algorithm design. They show that UIP is graph isomorphism hard, they chart a statistical zero-knowledge protocol for UIP, and they offer an algorithm that can compute all unimodular affine transformations between two polytopes. It’s a tour through a land where geometry, computation, and secrecy meet.
From graphs to polytopes: the unimodular isomorphism link
The authors’ first big move is to connect UIP to a famous computational challenge: graph isomorphism. If you can tell whether two graphs are the same up to renaming vertices, you’ve conquered a problem that sits in a curious place in complexity theory—it’s not known to be solvable in polynomial time, nor is it known to be NP-complete. Babai’s landmark quasi-polynomial time algorithm made waves by easing the barrier, but a full polynomial-time solution remains elusive.
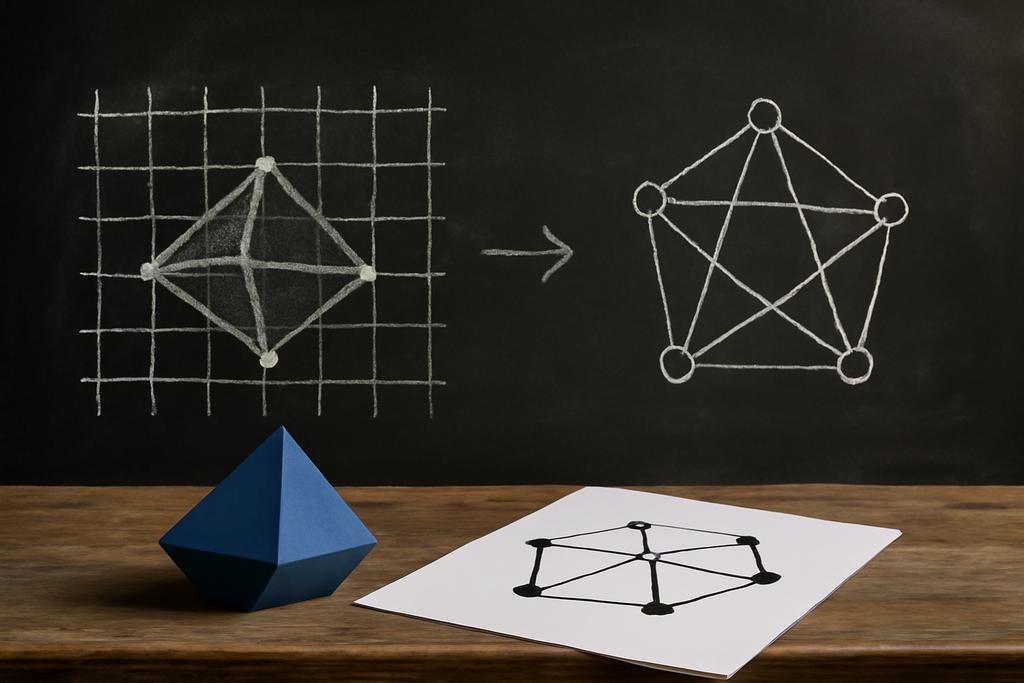
Here is the bridge Liu and Cai construct: for any graph G with n nodes, you can build an n-dimensional lattice polytope P(G) in a recipe that encodes the graph’s structure inside a geometric object. The vertices of P(G) include the origin, the standard basis vectors, and vectors that represent edges of the graph, specifically ei plus ej for each edge between i and j. The upshot is that if two graphs G and G prime are isomorphic, their corresponding polytopes P(G) and P(G prime) are unimodularly isomorphic. Conversely, if the polytopes P(G) and P(G prime) are unimodularly isomorphic, then the underlying graphs G and G prime must be isomorphic. In short, graph structure is woven into the very fabric of these polytopes.
The upshot is a concrete polynomial-time reduction from graph isomorphism to UIP. That means UIP inherits the same kind of hardness as graph isomorphism: it is not known to be easy in general, and solving UIP in full generality would imply a breakthrough on GI itself. This is a meaningful result because it places UIP squarely in a known complexity neighborhood, rather than as a purely abstract geometric curiosity. It also reframes questions about polytopes and their symmetries as questions about graph symmetry, which is a familiar and well-studied terrain for computer scientists.
Graph structure encoded inside a polytope is a theme that recurs in mathematical reduction work, and here it is done with a clarity that makes the UIP problem feel less like a nebulous geometric riddle and more like a decoding task you could actually study with a toolbox borrowed from graph theory.
A shield for the mind: zero knowledge for unimodular isomorphism
Beyond classification, the authors turn to a different kind of question: could you prove, without revealing the hidden transformation, that two polytopes are unimodularly isomorphic? The answer is yes, via a statistical zero-knowledge proof system inspired by lattice-based cryptography. In cryptographic terms, the prover can convince a verifier that a secret unimodular transformation exists, without ever exposing the transformation itself or the exact map between the polytopes.
The construction hinges on an average-case distribution that lives inside the unimodular isomorphism class of a polytope. Conceptually, you pick a representative P and then use Gaussian sampling, but in a way that respects the geometry encoded by the lattice. The trick is to produce samples that depend only on the isomorphism class, not on the particular curios that might leak the secret mapping. The authors build a protocol that looks like a standard Sigma protocol: the prover supplies a random sample drawn from the distribution, the verifier challenges with a random bit, and the prover responds with a witness that aligns with a candidate unimodular map if the challenge is honest. If the cheating player tries to cheat, the statistics collapse and the protocol fails with high probability.
Two aspects make this robust and compelling. First, the sampling uses discrete Gaussian distributions attached to the quadratic form that arises from the polytope in the chosen basis. This is a familiar tool in lattice-based cryptography, where noise and structured randomness help hide secrets while preserving mathematical relationships. Second, the protocol is built so that a simulated transcript is indistinguishable from a real one, even to an observer who knows nothing about the actual map. In the language of cryptography, this is a genuine zero-knowledge proof for UIP.
Discretely Gaussian sampling, popular in modern crypto, is not just a technical flourish here. It is a bridge between abstract geometry and practical security notions. The authors explicitly leverage a known exact sampler to guarantee the distribution’s properties, underscoring how ideas from different mathematical worlds can reinforce each other in surprising ways. The end result is not merely a curiosity about when two polytopes are the same; it is a blueprint for proving geometric equivalences without disclosing the secret route between them.
Zero knowledge in action here means a practical handshake between geometry and cryptography. You can verify that two shapes are related by a grid-preserving map without handing over the map itself, a capability that could be harnessed in future geometry-aware authentication or verification tasks in math-heavy workflows.
An algorithmic lens: enumerating all unimodular maps
If the GI barrier is a mountain, Liu and Cai also provide a path to climb it from the other side. They present an algorithm that, given two polytopes P and P prime with d vertices in dimension n, computes all unimodular affine transformations that map P to P prime. It is not merely existential: it is constructive. The algorithm builds a labeled graph GW(P) that encodes the combinatorial and geometric data of the polytope in a way that is friendly to algorithmic manipulation.
The labeling is clever. For each vertex v of P, they consider the adjacent vertices, compute the difference vectors to those neighbors, and assemble an n by n positive definite matrix Av from which the determinant det Av serves as a robust, unimodular-invariant label for that vertex. This label is preserved under any unimodular affine transformation. They extend this labeling to edges by summing the endpoint labels, producing a labeled graph GW(P) whose structure mirrors the polytope’s symmetries and geometry.
With these labels in hand, the problem of finding all unimodular maps is reduced to label-preserving isomorphisms between minimum spanning trees of the two labeled graphs. Why trees? Because a minimum spanning tree captures the essential skeleton of the graph with minimal total edge weight, sharply reducing the search space. Checking whether two labeled trees are isomorphic can be done efficiently with known algorithms, which the authors adapt to respect vertex labels. This is where the geometry meets a neat algorithmic trick: instead of brute-forcing all possible vertex correspondences, you lock onto the trees that best summarize the polytopes and look for label-respecting correspondences between them.
The payoff is practical and elegant. For polytopes with d vertices in dimension n, the approach runs in time polynomial in n and d, a nontrivial result given how quickly combinatorial explosions can appear in high-dimensional geometry. The method also tames the automorphism group that can arise from symmetry, using a tree centroid decomposition to enumerate label-preserving automorphisms efficiently. In symmetric cases, this prevents an explosion of candidate maps that would waste precious compute time.
Put simply, their algorithm tells you not only whether P and P prime are unimodularly isomorphic, but exactly which transformations realize that relation. It is a constructive answer to UIP, grounded in a synthesis of graph theory, linear algebra, and lattice geometry. The practical implication is a new toolbox for classifying lattice polytopes, a key pursuit in discrete geometry and a stepping stone toward Arnold-like questions about the diversity of such polytopes across dimensions and volumes.
polynomial-time path through a problem that has seemed unwieldy at first glance shows how careful modeling and a dash of classical graph theory can unlock previously intractable corners of geometry. This isn’t just theoretical elegance; it’s a blueprint for systematic, scalable exploration of high-dimensional lattice shapes.
From a broader perspective, the Li u Cai work sits at a crossroads. It reinforces the viewpoint that geometry on the lattice and combinatorial structure can simulate graphs, while also showing that modern cryptographic techniques can illuminate questions in pure geometry. The result is a two-way street: complexity theory informs what we can and cannot hope to compute about polytopes, and geometry-inspired constructions provide new avenues for cryptographic ideas such as zero-knowledge proofs that are robust in average-case settings.
As with many mathematical threads, the practical significance is not merely in solving a single problem but in weaving a framework that can be extended. UIP, its GI-hardness, the zero-knowledge protocol, and the constructive algorithm all contribute to a shared language for talking about when two lattice shapes are the same under grid-preserving rules. And in a world where discrete geometry keeps nudging into applications—data science, optimization, cryptography, materials science—the ability to recognize and certify such equivalences with rigor and security is a valuable currency.
These advances come from Tianjin University, where Liu and Cai map out a landscape that marries rigorous math with computational practicality. It is a reminder that modern mathematics is not just about proving theorems in isolation but about building interoperable tools that speak across disciplines. The unimodular isomorphism problem becomes, in their hands, a focal point where geometry, algorithms, and cryptography illuminate one another, with the promise of new insights into how shapes, grids, and graphs mirror each other across the mathematical universe.
In the end, the question lingering after reading this work is not simply whether two polytopes are the same under a grid-respecting map. It is what happens when a family of problems that look purely geometric reveals itself to be another language for graph symmetry, security, and computation. The answer, as Liu and Cai show, is a chorus of connections—between a simple yet powerful transformation, the stubborn hardness of GI, and the practical machinery of zero-knowledge proofs. The shapes on the lattice are not just abstract curiosities; they are a proving ground for ideas that could influence how we prove, verify, and even trust the mathematics that underpins the digital world.