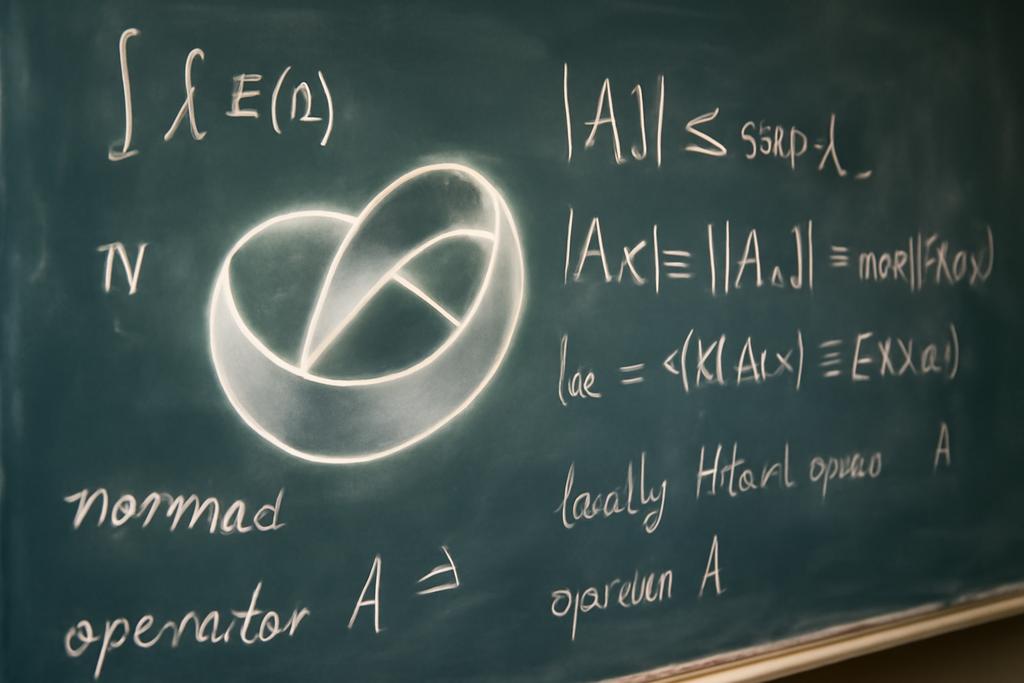Delving into the Unseen Depths of Locally Normal Operators
Imagine a world beyond the familiar landscapes of finite-dimensional vector spaces. A realm where operators, those mathematical transformers of data, roam across infinitely complex territories. This is the domain of locally Hilbert spaces, and within it, a new mathematical breakthrough has begun to reshape our understanding of spectral theory.
For years, mathematicians have struggled with the complexities of locally normal operators – operators that are both normal (meaning their behavior is predictable in a specific sense) and operate within these infinite-dimensional, locally Hilbert spaces. These spaces are built as layers of increasingly complex Hilbert spaces, each nestled within the next, extending infinitely. Thinking of it like a Russian nesting doll helps visualize this infinite growth. The difficulty arises from the absence of a singular, overarching structure to grasp their behavior. Their properties are inherently local, spread across this infinite hierarchy, making them extremely difficult to analyze using traditional techniques.
A recent paper by Aurelian Gheondea, based at the Institutul de Matematic˘a al Academiei Romˆane and Bilkent University, tackles this very challenge. He presents a powerful new spectral theorem, offering a unified framework for understanding the spectral properties of these elusive operators. The spectral theorem, in simpler terms, is a technique that allows one to decompose complex operators into simpler building blocks, much like a complex piece of music can be broken down into its individual notes. The beauty and significance of the theorem lie in its ability to apply to this infinitely layered structure, which has been previously intractable.
The Limitations of Traditional Approaches
Traditional spectral theorems, honed for finite-dimensional spaces and simpler infinite-dimensional ones, fail to adequately address the nuances of locally normal operators in locally Hilbert spaces. These theorems rely on a global structure that simply doesn’t exist in this infinite nesting of Hilbert spaces. The characteristics of these operators aren’t immediately apparent at a glance—they’re scattered throughout the infinite hierarchy of spaces, making them challenging to capture with familiar mathematical tools.
Gheondea’s work elegantly circumvents this limitation. Instead of searching for a singular, global description, he constructs a series of representations, each valid within a specific “layer” of the locally Hilbert space. This approach allows him to combine local descriptions into a coherent, global understanding. He employs what are known as inductive and projective limits, advanced mathematical tools that stitch together the individual layer descriptions into a meaningful whole—like weaving together threads to create a tapestry.
The Power of Inductive and Projective Limits
Inductive and projective limits are powerful mathematical constructs. Imagine them as sophisticated assembly instructions, allowing one to build intricate structures from simpler components. In Gheondea’s work, these tools deftly handle the infinite nesting of Hilbert spaces. Inductive limits “build up” the overall structure, while projective limits provide a means of analyzing the infinite extension of that structure, allowing for an unprecedented understanding of the behavior of these operators.
The paper masterfully employs these concepts to tackle two types of representations: functional models and direct integral representations. Functional models, in essence, translate the behavior of the operator into the properties of functions—a simpler, more intuitive realm to work with. Direct integral representations offer another method, decomposing the locally Hilbert space itself into smaller parts, where the behavior of the operator becomes clearer.
The Hata Tree: An Unexpected Connection
One of the most surprising and elegant aspects of Gheondea’s research is its connection to the Hata tree, a specific self-similar fractal. Self-similar fractals are striking geometrical objects whose parts resemble the whole, exhibiting a kind of recursive structure. The Hata tree, a particular kind of fractal structure, serves as an illustrative example in Gheondea’s work.
By applying his spectral theorem to this fractal structure, Gheondea demonstrates the versatility and broad applicability of his approach. The presence of a fractal example shows the potential application of his theorems extends beyond pure mathematical theory into the world of fractals and potentially other areas of mathematics that involve intricate and recursive structures.
Implications and Future Directions
Gheondea’s work is not merely a theoretical exercise. It opens avenues for further investigation into the spectral theory of locally normal operators and potentially other operators in locally Hilbert spaces. This could offer novel techniques for analyzing complex systems that are beyond the reach of current tools, particularly those systems with deeply nested or recursive structures.
The connection to fractals, in particular, hints at potential applications in areas such as image processing and quantum mechanics—both fields that deal extensively with intricate, self-similar patterns. The broader implications of this work are still unfolding, but it lays the groundwork for a deeper understanding of the infinite-dimensional spaces and the operators that inhabit them.
Furthermore, Gheondea’s research raises fundamental questions about the relationship between local and global properties in infinite-dimensional spaces. This exploration could yield deeper insights into the nature of infinity itself, and the way that we as humans can come to understand and conceptualize infinity.